agen_pale
New member

Seringkah kalian berbelanja di swalayan atau di warung dekat rumahmu? Cobalah kalian perhatikan barang-barang yang dijual.
Barang-barang yang dijual biasanya dihimpun sesuai jenisnya. Penghimpunan jenis barang dapat memudahkan pembeli memilih barang.
Jadi, tahukah kalian apa kegunaan himpunan?
Untuk memahami tentang himpunan marilah kita pelajari materi ini dengan saksama.
1. Pengertian HIMPUNAN
Himpunan adalah
kumpulan benda atau objek yang dapat didefinisikan dengan jelas, sehingga dengan tepat dapat diketahui objek yang termasuk himpunan dan yang tidak termasuk dalam himpunan tersebut.
Sekarang perhatkan contoh berikut ini :
a. Kumpulan Lukisan indah
b. Kumpulan wanita cantik Indonesia
Kumpulan lukisan indah tidak dapat disebut himpunan, karena lukisan indah menurut seseorang belum tentu indah menurut orang lain. Dengan kata lain, kumpulan lukisan indah tidak dapat didefinisikan dengan jelas.
Demikian halnya dengan kumpulan wanita cantik di Indonesia. Wanita cantik menurut seseorang belum tentu cantik menurut orang lain. Jadi, kumpulan wanita cantik bukan termasuk himpunan.
2. NOTASI HIMPUNAN
Suatu himpunan biasanya diberi nama atau dilambangkan dengan huruf besar (kapital) A, B, C, ..., Z. Adapun benda atau objek yang termasuk dalam himpunan tersebut ditulis dengan menggunakan pasangan kurung kurawal {...}.
Setiap benda atau objek yang berada dalam suatu himpunan disebut anggota atau elemen dari himpunan itu dan dinotasikan dengan
Contoh Soal :
Nyatakan himpunan berikut dengan memberikan tanda kurung kurawal :
1. A adalah himpunan bilangan cacah kurang dari 6
2. P adalah himpunan huruf-huruf vokal
3. Q adalah himpunan tiga binatang buas
Jawab :
A adalah himpunan bilangan cacah kurang dari 6.
Anggota himpunan bilangan cacah kurang dari 6 adalah 0, 1, 2, 3, 4, 5.
Jadi, A = {0, 1, 2, 3, 4, 5}.
P adalah himpunan huruf-huruf vokal.
Anggota himpunan huruf-huruf vokal adalah a, e, i, o, dan u, sehingga ditulis
P = {a, e, i, o, u}.
Q adalah himpunan tiga binatang buas.
Anggota himpunan binatang buas antara lain harimau, singa, dan serigala.
Jadi, Q = {harimau, singa, serigala}.
Banyak anggota suatu himpunan dinyatakan dengan n. Jika A = {0, 1, 2, 3, 4, 5} maka n(A) = banyak anggota himpunan A = 6. Banyaknya anggota himpunan A dinyatakan dengan n(A).
Dalam matematika, beberapa huruf besar digunakan sebagai lambang himpunan bilangan tertentu, di antaranya sebagai berikut :
|-
|width="75"; align="center"|Huruf A
|Lambang himpunan bilangan asli. A = {1, 2, 3, 4, ... }
|-
|align="center"|Huruf B
|Lambang himpunan bilangan bulat. B = {..., –3, –2, –1, 0, 1, 2, 3, ...}
|-
|align="center"|Huruf C
|Lambang himpunan bilangan cacah. C = {0, 1, 2, 3, ... }
|-
|align="center"|Huruf L
|Lambang bilangan ganjil. L = {1, 3, 5, 7, 9, 11, 13, ...}
|-
|align="center"|Huruf N
|Lambang bilangan genap. N = { 12, 14, 20, 24, ...}
|-
|align="center"|Huruf Q
|Lambang bilangan rasional
|-
3. Menyatakan Suatu Himpunan
Suatu himpunan dapat dinyatakan dengan tiga cara sebagai berikut :
a. Dengan kata-kata
Dengan cara menyebutkan semua syarat / sifat keanggotaannya.
Contoh :
P adalah himpunan bilangan prima antara 10 dan 40
di tulis P = { bilangan prima antara 10 dan 40}
Contoh :
P adalah himpunan bilangan prima antara 10 dan 40
di tulis P = { bilangan prima antara 10 dan 40}
b. Dengan notasi pembentuk himpunan
Sama seperti menyatakan himpunan dengan kata-kata, pada cara ini disebutkan semua syarat/sifat keanggotannya. Namun, anggota himpunan dinyatakan dengan suatu peubah. Peubah yang biasa digunakan adalah x atau y.
Contoh :
P : {bilangan prima antara 10 dan 40}.
Dengan notasi pembentuk himpunan, ditulis
P = {10 < x < 40, x
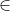 bilangan prima}.
bilangan prima}.
Contoh :
P : {bilangan prima antara 10 dan 40}.
Dengan notasi pembentuk himpunan, ditulis
P = {10 < x < 40, x
c. Dengan mendaftar anggota-anggotanya
Dengan cara menyebutkan anggota-anggotanya, menuliskannya
dengan menggunakan kurung kurawal, dan anggotaanggotanya
dipisahkan dengan tanda koma.
Contoh :
P = {11, 13, 17, 19, 23, 29, 31, 37}
A = {1, 2, 3, 4, 5}
dengan menggunakan kurung kurawal, dan anggotaanggotanya
dipisahkan dengan tanda koma.
Contoh :
P = {11, 13, 17, 19, 23, 29, 31, 37}
A = {1, 2, 3, 4, 5}
bersambung....